انظر إلى هذا الرقم: 6174.
قد لا يبدو بعد النظرة الأولى كبيرا، لكنه حيرعلماء الرياضياتوالمتحمسين للأرقام واللعب بها منذ عام 1949.
لماذا؟ تمعن في الحقائق التالية واحكم بنفسك:
اختر أربعة أرقام، أي أرقام تريدها، بشرط أن يكون اثنان منها على الأقل مختلفين (ومن ضمنها الصفر). فنفرض مثلا أنك اخترت 1234
رتب الأرقام تنازليا:4321
الآن رتبها تصاعديا:1234
اطرحالرقم الأصغرمن الرقم الأكبر:4321 - 1234
الآن أعد الخطوات 2 و3 و4 معالنتيجةالتي ستحصل عليها
تعالوا نجرب العملية معا

 

4321 - 1234 =3087
نرتب الأرقام تنازليا:8730
ثم نرتبها تصاعديا:0378
نطرحالرقم الأصغرمن الرقم الأكبر: 8730 - 0378 =8352
فلنعد الخطوات الثلاث معالنتيجةالتي نحصل عليها
والآن نحاول مع8352
8352 - 2358 =6174
وأعد مرة أخرى الخطوات نفسها مع6174، بترتيب الأرقام تنازليا، وتصاعديا، ثم اطرحالرقم الأصغرمن الأكبر
7641 - 1467 =6174

وهكذا ترى أننا إذا واصلنا تلك الخطوات فستكونالنتيجةهي نفسها، فسوف نحصل علىالنتيجةنفسها، وهي الرقم:6174
وربما تعتقد أن ما حدث كان مصادفة. دعنا إذن نجرب العملية مع رقم عشوائي آخر. ما رأيك في2005؟

5200 - 0025 =5175
7551 - 1557 =5994
9954 - 4599 =5355
5553 - 3555 =1998
9981 - 1899 =8082
8820 - 0288 =8532
8532 - 2358 =6174
7641 - 1467 =6174
وهكذا نجد أنالنتيجةواحدة، بغض النظر عن الأرقام الأربعة التي تختارها، فسوف تنتهي إلى6174، ومنها أيضا ستتوصل إلى نفس النتيجة
النتيجة الثابتة لكابريكار

 

تهانينا، فقد تعرفت الآن علىالنتيجةالثابتة لكابريكار.
كان عالم الرياضيات الهندي، داتاريا رامتشاندرا كابريكار (1905-1986) يحب اللعب بالأرقام، وبهذه الطريقة توصل إلى جمال لغز الرقم6174.

وقدم كابريكار، الذي يقر بأنه مدمن للأرقام، اكتشافه إلىالعالمفي مؤتمر للرياضيات عقد في مدينة مادراس في 1949.

وكان معتادا أن يقول "إذا أراد سكير مواصلة شرب النبيذ حتى يبقى في حالة انتعاش، فإن حاله مثل حالتي مع الأرقام".

ودرس كابريكار في جامعة مومباي وقضى حياته معلما في مدرسة في بلدة ديفلالي الصغيرة في الهند، في تلال مومباي الشمالية.

وعلى الرغم مما واجهه من سخرية ورفض من قبلعلماء الرياضياتفي الهند، الذين رأوا أن عمله تافه وغير مهم، فإنه كان كاتبا غزير الإنتاج، خاصة في المنشورات العلمية.

وكان غالبا ما يُدعى إلى المشاركة في المؤتمرات، أو الحديث في المدارس والكليات عن طرقه العجيبة وملاحظاته المبهرة عن الأرقام.
من يضحك أخيرا ..

 

بدأت أفكار كابريكار بالتدريج تنال الأعجاب في بلاده وفي الخارج. وبحلول السبعينيات، كتب عنه المؤلف الأمريكي الذائع الصيت، والمتحمس للرياضيات، مارتن غاردنر، مقالة في مجلة (ساينتيفيك أمريكا).

وأصبحالعالماليوم يعترف بكابريكار ومكتشفاته، التي يتداولها الناس في أنحاء العالم، خاصة من لا يستطيعون مقاومة اللعب بالأرقام مثله.
ويقول البروفيسور، يوتاكا نيشياما، الذي يعمل في جامعة أوساكا للاقتصاد: "رقم6174هو فعلا رقم ملغز".

وشرح نيشياما في مقالة في مجلة (+ بلس) كيف أنه استخدم الكمبيوتر للتحقق مما إذا كانت العمليات الحسابية على جميع الأرقام الأربعة وصلت إلى الرقم6174في عدد محدود من الخطوات".
وماذا وجد؟ تفضي أي أربعة أرقام، بحيث لا تكون كلها متساوية، إلى6174بناء على عملية كابريكار في سبع خطوات على الأكثر.
ويقول نيشياما: "إن لم تصل إلى6174بعد استخدام عملية كابريكار سبع مرات، فلابد أنك ارتكبت خطأ في حساباتك، وعليك أن تحاول مرة أخرى".

أرقام سحرية

وربما يثير تعجبك عدد الأرقام الأخرى "الخاصة"، ترى، كم هي؟ والإجابة هي .. لا نعرف بالتأكيد.
ولكن ما نعرفه هو أن هناك ظواهر مماثلة مثل عملية كابريكار الثابتةالنتيجةبالنسبة إلى ثلاثة أرقام.
دعونا نجرب. يمكن أن نبدأ بأي ثلاثة أرقام عشوائيا، مثل574:
574 - 457 =297

972 - 279 =693
963 - 369 =594
954 - 459 =495
954 - 459 =495
وهكذا توصلنا إلى: "رقم سحري" آخر هو:495.

6174 بألوان مختلفة

قررتمؤسسةسيغرام للتكنولوجيا في الهند، والتي يوجد مقرها في مومباي، والتي طورت "منبرا لتكنولوجيا المعلومات" للمدارس في الريف والحضر، أن تأخذ الرقم6174وتلعب بالأرقام والألوان.
وقال مؤسس الشركة، غريش أرابيل، لبي بي سي إنه يحرص دائما على تحفيز أطفال المدارس، خاصة من يكره الرياضيات منهم، وإنه يريد أن يريهم أن هناك متعة فيها.

ويقول أرابيل: "ثباتالنتيجةفي عمليات كابريكار شي جميل. عندما تتبع الخطوات، فإنها تقودك إلى الوصول إلى لحظة رائعة. وهذا لا يحدث دائما حينما نتعلم مستخدمين مناهج الرياضيات التقليدية".

وقرر فريق أرابيل، وكل هذا في أذهانهم، أن يلونوا الخطوات التي توصل إلى الرقم6174- آخذين في الاعتبار أن العملية لا تأخذ أكثر من سبع خطوات للوصول إلى الرقم "السحري".
أصبح هذا هو الأساس لشفرة يمكن إعادة استخدامها بسهولة في أجهزة كمبيوتر راسبيري باي aspberry Pi البسيطة التركيب والمنخفضة التكلفة، والتي لا تزيد على حجم بطاقة الائتمان، وهي أداة شائعة في تدريس العلوم والتكنولوجيا والهندسة والرياضيات.

ويستطيع الطلاب في ذلك استخدام لغة ولفرام، وهي لغة برمجة متعددة النماذج الحسابية، وتوجد مجانا على أجهزة راسبيري باي، وتجري العمليات الحسابية لجميع مجموعات الأرقام الأربعة الموجودة، وعددها 10000 مجموعة.
وأدى ذلك إلى خلق أنماط باتباع نفس عدد الخطوات المطلوبة للوصول إلى رقم6174، ورتبت ذلك في جدول متعدد الألوان.


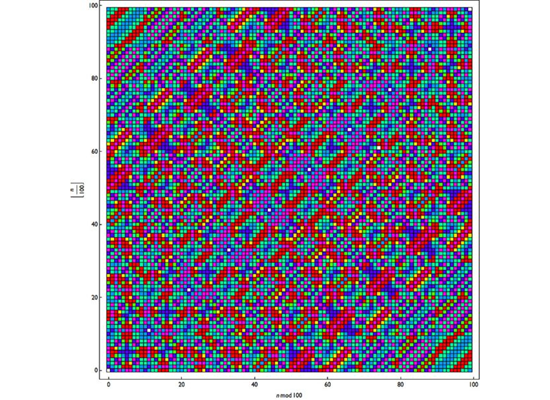
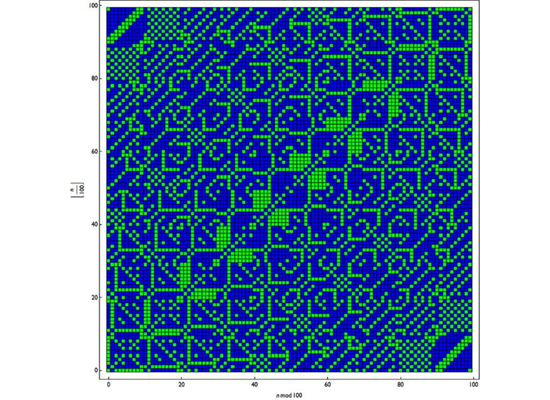
وبعد بدء العملية الحسابية، ما الذي تستطيع أن تراه إذا وضعت الأعداد الفردية باللون الأزرق، والأعداد الزوجية باللون الأخضر؟

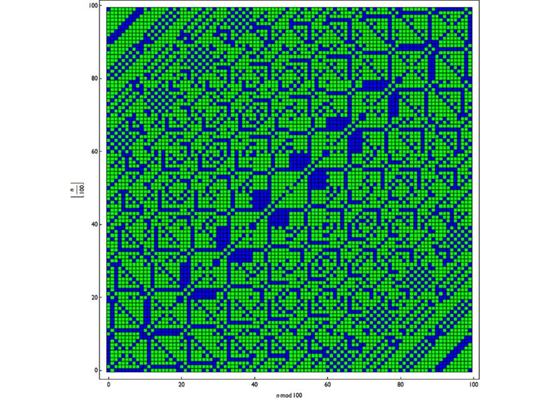
وإذا وضعت الأعداد الأولية باللون الأخضر، وبقية الأعداد باللون الأزرق، فماذا ترى؟ وهل سيتغير النمط كثيرا؟


الرياضيات الترفيهية




سكاي نيوز